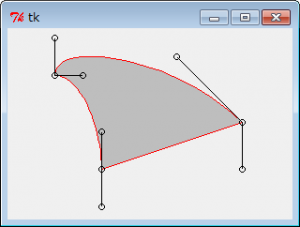
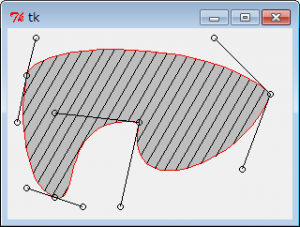
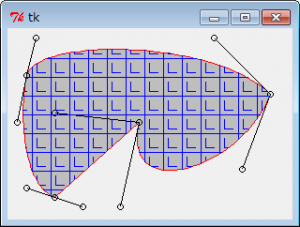
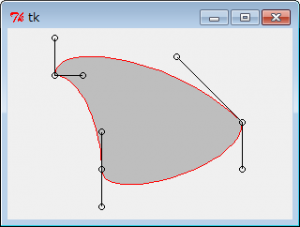
前回も理想のドローソフトについての記事でしたが、今だその熱を持っていて、今回はパスとかハッチングとかやってみました。
EMFやSVGなどに出力することを考えると、ライブラリが持つ機能に依存するよりは、なるだけ自前で実装したほうが良いはず。どちらのファイル形式もベジェ曲線はサポートしているので、3次ベジェ曲線によるパスのプログラミングを試みました。
ドローソフトと言えばこれだよね。
[ソース1](ソースは最後にあります)
機能として必須なのが、パターンハッチング。
ベジェ曲線と直線の交点の計算なんてどうやるんだーっと思ったけど、情報を載せてくれる人はいるもんですなぁ。ありがたい。
5(その2):直線と曲線の交点(解の公式)
これで直線ならどんな模様でもできる。いずれ楕円も加えたい。
虚数とか出てきてなかなか大変でしたが、出張により久々に一人の夜を過ごし、たっぷり作業できたので、なんとか形にはなりました(後々不具合が出てくるのは必至だと思いますが)。久しぶりにがっつりプログラミング、楽しい。
次にしたいと思っているのが、ブーリアン演算による差分とか合成とか。果たして僕の能力が及ぶのか。。。
[ソース1:ベジェ曲線パス]
# -*- coding: utf-8 -*-
import Tkinter
class Node:
p = [0.0,0.0] #self point
p0 = [0.0,0.0] #control point
p1 = [0.0,0.0] #control point
p0_avoid = False
p1_avoid = False
def __init__(self,p,p0,p1):
self.p = p
self.p0 = p0
self.p1 = p1
class Path:
nodes = []
closed = False
steps = 20
def __init__(self,nodes = None):
if nodes == None:
return
self.nodes = nodes
def points(self):
if len(self.nodes) == 0:
return []
points = []
points.append(self.nodes[0].p)
for i in range(1,len(self.nodes)):
points += self._segment_points(i-1,i)
if self.closed:
points += self._segment_points(i,0)
points = points[:-1]
return points
def _segment_points(self,i,j):
points = []
n0 = self.nodes[i]
n1 = self.nodes[j]
if n0.p1_avoid == True and n1.p0_avoid == True:
points.append(n1.p)
else:
pts = self.bezier_curve_points(n0.p,n0.p1,n1.p0,n1.p)
points += pts[1:]
return points
def bezier_curve_points(self,p0,p1,p2,p3):
points = []
for i in range(self.steps+1):
t = float(i)/self.steps
x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
points.append((x,y))
return points
def main():
window = Tkinter.Tk()
canvas = Tkinter.Canvas(window,width=300,height=200)
canvas.pack()
n0 = Node([50,50],[50,10],[80,50])
n1 = Node([100,150],[100,110],[100,190])
n2 = Node([250,100],[250,150],[180,30])
path = Path([n0,n1,n2])
path.closed = True
#n1.p1_avoid = True
#n2.p0_avoid = True
if path.closed:
canvas.create_polygon(path.points(),fill='gray',outline='red')
else:
canvas.create_line(path.points(),fill='red')
r = 3
for n in path.nodes:
canvas.create_oval(n.p[0]-r,n.p[1]-r,n.p[0]+r,n.p[1]+r)
canvas.create_oval(n.p0[0]-r,n.p0[1]-r,n.p0[0]+r,n.p0[1]+r)
canvas.create_oval(n.p1[0]-r,n.p1[1]-r,n.p1[0]+r,n.p1[1]+r)
canvas.create_line(n.p[0],n.p[1],n.p0[0],n.p0[1])
canvas.create_line(n.p[0],n.p[1],n.p1[0],n.p1[1])
window.mainloop()
if __name__ == '__main__':
main()
[ソース2:斜線ハッチング]
# -*- coding: utf-8 -*-
import math
import Tkinter
class Node:
p = [0.0,0.0] #self point
p0 = [0.0,0.0] #control point
p1 = [0.0,0.0] #control point
p0_avoid = False
p1_avoid = False
def __init__(self,p,p0,p1):
self.p = p
self.p0 = p0
self.p1 = p1
class Path:
nodes = []
closed = False
steps = 20
def __init__(self,nodes = None):
if nodes == None:
return
self.nodes = nodes
def points(self):
if len(self.nodes) == 0:
return []
points = []
points.append(self.nodes[0].p)
for i in range(1,len(self.nodes)):
points += self._segment_points(i-1,i)
if self.closed:
points += self._segment_points(i,0)
points = points[:-1]
return points
def _segment_points(self,i,j):
points = []
n0 = self.nodes[i]
n1 = self.nodes[j]
if n0.p1_avoid == True and n1.p0_avoid == True:
points.append(n1.p)
else:
pts = self.bezier_curve_points(n0.p,n0.p1,n1.p0,n1.p)
points += pts[1:]
return points
def bezier_curve_points(self,p0,p1,p2,p3):
points = []
for i in range(self.steps+1):
t = float(i)/self.steps
x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
points.append((x,y))
return points
class PattanStripe:
degree = -55 # -90 <= degree <= 90
lines = []
space = 10
def __init__(self,path):
self.path = path
self.update()
def update(self):
#range
area = [float('inf'),float('inf'),0.0,0.0] #xmin,ymin,xmax,ymax
for p in self.path.points():
if area[0] > p[0]: area[0] = p[0]
elif area[2] < p[0]: area[2] = p[0]
if area[1] > p[1]: area[1] = p[1]
elif area[3] < p[1]: area[3] = p[1]
#lines
lines = []
sp = self.space
if self.degree == 90 or self.degree == -90:
a = 1.0
b = 0.0
count = int((area[2]-area[0])/sp+1)
for n in range(count):
x = area[0] +sp*n -sp/2
c = -x
lines.append((a,b,c))
else:
a = math.tan(math.radians(self.degree))
b = -1.0
sp = abs(sp/math.cos(math.radians(self.degree)))
dy = abs(a*(area[2]-area[0]))
count = int(abs(area[3]-area[1]+dy)/sp+1)
if a < 0:
start_y = area[1]-sp/2
else:
start_y = area[1]-dy-sp/2
x = area[0]
for n in range(count):
y = start_y +sp*n
c = -a*x -b*y
lines.append((a,b,c))
#cut lines
self.lines = []
self.cross_points = []
nodes = self.path.nodes + [self.path.nodes[0]]
for line in lines:
cross = []
for i in range(len(self.path.nodes)):
p0 = nodes[i].p
p1 = nodes[i].p1
p2 = nodes[i+1].p0
p3 = nodes[i+1].p
if (nodes[i].p1_avoid == True and
nodes[i+1].p0_avoid == True):
pts = intersection_of_line_segment(p0,p3,line)
else:
pts = intersection_of_bezier_and_line((p0,p1,p2,p3),line)
cross += pts
self.cross_points += cross #for debug
if len(cross) % 2 != 0:
print('error Pattan update()')
continue
cross.sort()
for j in range(0,len(cross),2):
new_line = cross[j] + cross[j+1]
self.lines.append(new_line)
def intersection_of_line_segment((x0,y0),(x1,y1),(a,b,c)):
line = line_generalization((x0,y0),(x1,y1))
points = intersection_2line(line,(a,b,c))
m = 0.000001
xs = [x0,x1]
ys = [y0,y1]
new_points = []
for p in points:
if (min(xs)-m <= p[0] and p[0] <= max(xs)+m and
min(ys)-m <= p[1] and p[1] <= max(ys)+m):
new_points.append(p)
return new_points
def intersection_2line((a0,b0,c0),(a1,b1,c1)):
t = float(a0*b1-a1*b0)
if t == 0:
return []
x = (b0*c1-b1*c0)/t
y = (a1*c0-a0*c1)/t
return [(x,y)]
def intersection_of_bezier_and_line((p0,p1,p2,p3),(a,b,c)):
f0 = a * p0[0] + b * p0[1] + c
f1 = 3 * (a * p1[0] + b * p1[1] + c)
f2 = 3 * (a * p2[0] + b * p2[1] + c)
f3 = a * p3[0] + b * p3[1] + c
_a = -f0 + f1 - f2 + f3
_b = 3 * f0 - 2 * f1 + f2
_c = -3 * f0 + f1
_d = f0
if _a == 0:
if _b == 0:
if _c == 0: tlist = []
else: tlist = -_d/_c
else:
tlist = quadratic_equation(_b,_c,_d)
else:
tlist = cubic_equation(_a,_b,_c,_d)
points = []
for t in tlist:
if t < 0 or 1 < t:
continue
x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
points.append((x,y))
return points
def cubic_equation(a,b,c,d):
p = -b**2/(9.0*a**2) + c/(3.0*a)
q = b**3/(27.0*a**3) - b*c/(6.0*a**2) + d/(2.0*a)
t = complex(q**2+p**3)
w =(-1.0 +1j*3.0**0.5)/2.0
u = [0,0,0]
u[0] = (-q +t**0.5)**(1.0/3.0)
u[1] = u[0] * w
u[2] = u[0] * w**2
v = [0,0,0]
v[0] = (-q -t**0.5)**(1.0/3.0)
v[1] = v[0] * w
v[2] = v[0] * w**2
x_list = []
for i in range(3):
for j in range(3):
if abs(u[i]*v[j] + p) < 0.0001:
x = u[i] + v[j]
if abs(x.imag) < 0.0000001:
x = x.real - b/(3.0*a)
x_list.append(x)
return x_list
def quadratic_equation(a,b,c):
d = b*b-4*a*c
if d < 0:
return []
if d == 0:
x = -b/(2.0*a)
return [x]
else:
x0 = (-b+d**0.5)/(2.0*a)
x1 = (-b-d**0.5)/(2.0*a)
return [x0,x1]
def line_generalization(p0,p1):
if p0[0] == p1[0]:
a = 1.0
b = 0.0
c = float(-p0[0])
elif p0[1] == p1[1]:
a = 0.0
b = 1.0
c = float(-p0[1])
else:
slope = float(p1[1]-p0[1])/(p1[0]-p0[0])
intercept = p0[1] - slope*p0[0]
a = slope
b = -1.0
c = intercept
return a,b,c
def main():
window = Tkinter.Tk()
canvas = Tkinter.Canvas(window,width=300,height=200)
canvas.pack()
n0 = Node([20,50],[30,10],[10,100])
n1 = Node([50,180],[20,170],[80,190])
n2 = Node([140,100],[50,90],[120,190])
n3 = Node([280,70],[250,150],[220,10])
path = Path([n0,n1,n2,n3])
path.closed = True
#n1.p1_avoid = True
#n2.p0_avoid = True
path.pattan = PattanStripe(path)
if path.closed:
canvas.create_polygon(path.points(),fill='gray',outline='red')
else:
canvas.create_line(path.points(),fill='red')
r = 3
for n in path.nodes:
canvas.create_oval(n.p[0]-r,n.p[1]-r,n.p[0]+r,n.p[1]+r)
canvas.create_oval(n.p0[0]-r,n.p0[1]-r,n.p0[0]+r,n.p0[1]+r)
canvas.create_oval(n.p1[0]-r,n.p1[1]-r,n.p1[0]+r,n.p1[1]+r)
canvas.create_line(n.p[0],n.p[1],n.p0[0],n.p0[1])
canvas.create_line(n.p[0],n.p[1],n.p1[0],n.p1[1])
for xy in path.pattan.lines:
canvas.create_line(xy)
r = 2
for p in path.pattan.cross_points:
#canvas.create_oval(p[0]-r,p[1]-r,p[0]+r,p[1]+r)
pass
window.mainloop()
if __name__ == '__main__':
main()
[ソース3:パターンハッチング]
# -*- coding: utf-8 -*-
#import math
import Tkinter
class Node:
p = [0.0,0.0] #self point
p0 = [0.0,0.0] #control point
p1 = [0.0,0.0] #control point
p0_avoid = False
p1_avoid = False
def __init__(self,p,p0,p1):
self.p = p
self.p0 = p0
self.p1 = p1
class Path:
nodes = []
closed = False
steps = 50
def __init__(self,nodes = None):
if nodes == None:
return
self.nodes = nodes
def points(self):
if len(self.nodes) == 0:
return []
points = []
points.append(self.nodes[0].p)
for i in range(1,len(self.nodes)):
points += self._segment_points(i-1,i)
if self.closed:
points += self._segment_points(i,0)
points = points[:-1]
return points
def _segment_points(self,i,j):
points = []
n0 = self.nodes[i]
n1 = self.nodes[j]
if n0.p1_avoid and n1.p0_avoid:
points.append(n1.p)
else:
pts = self.bezier_curve_points(n0.p,n0.p1,n1.p0,n1.p)
points += pts[1:]
return points
def bezier_curve_points(self,p0,p1,p2,p3):
points = []
for i in range(self.steps+1):
t = float(i)/self.steps
x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
points.append((x,y))
return points
class PattanTile:
width = 20
height = 20
polylines = []
lines = []
cross_points = []
xn = 0
yn = 0
def __init__(self,path):
self.path = path
self.polylines = [[0,0,0,20,20,20,20,0,0,0],[5,5,5,15,15,15]]
self.update()
def setPattan(self,width,height,polylines):
self.width = width
self.height = height
self.polylines = polylines
def update(self):
area = self._area( self.path.points())
self.xn = int((area[2]-area[0])/self.width)+1
self.yn = int((area[3]-area[1])/self.height)+2
tiles = [[[0,0,0,0] for j in range(self.yn)] for i in range(self.xn)]
tiles = self._tile_cross_points(tiles,area)
tiles = self._tile_states(tiles)
self.lines = self._lines(tiles)
def _area(self,points):
area = [float('inf'),float('inf'),0.0,0.0] #xmin,ymin,xmax,ymax
for p in points:
if area[0] > p[0]: area[0] = p[0]
elif area[2] < p[0]: area[2] = p[0]
if area[1] > p[1]: area[1] = p[1]
elif area[3] < p[1]: area[3] = p[1]
return area
def _tile_cross_points(self,tiles,area):
nodes = self.path.nodes + [self.path.nodes[0]]
sx = area[0]-self.width/2
sy = area[1]-self.height/2
for i in range(self.xn):
for j in range(self.yn):
x0 = sx + self.width*i
y0 = sy + self.height*j
x1 = x0 + self.width
y1 = y0 + self.height
blines = [(x0,y0,x0,y1),(x0,y0,x1,y0),
(x1,y0,x1,y1),(x0,y1,x1,y1)]
cross_points = []
for border_line in blines:
cross_points += self.crossPointsOfPath(border_line)
tile = [x0,y0,0,len(cross_points)]
tiles[i][j] = tile
self.cross_points += cross_points
return tiles
def _tile_states(self,tiles):
tile_states = [[0 for j in range(self.yn)] for i in range(self.xn)]
for i in range(self.xn):
for j in range(self.yn):
cross_point_n = tiles[i][j][3]
if cross_point_n > 1:
tile_states[i][j] = 4 #on border
for i in range(self.xn):
for j in range(self.yn):
state = tile_states[i][j]
if state > 0:
continue
self._bflag = False
tile_states = self._tile_fill(i,j,tile_states)
if self._bflag:
state = 2 #outside path
else:
state = 3 #inside path
for k in range(self.xn):
for l in range(self.yn):
if tile_states[k][l] == 1:
tile_states[k][l] = state
for i in range(self.xn):
for j in range(self.yn):
tiles[i][j][2] = tile_states[i][j]
return tiles
def _lines(self,tiles):
lines = []
for i in range(self.xn):
for j in range(self.yn):
state = tiles[i][j][2]
if state == 3: #inside path
lines += self._pattan_lines(tiles[i][j])
elif state == 4: #on border
_lines = self._pattan_lines(tiles[i][j])
lines += self._trim_lines(_lines)
return lines
def _pattan_lines(self,tile):
x,y,s,cpts = tile
pattan_lines = []
for polyline in self.polylines:
for k in range(0,len(polyline)-2,2):
x0 = x + polyline[k]
y0 = y + polyline[k+1]
x1 = x + polyline[k+2]
y1 = y + polyline[k+3]
line = [x0,y0,x1,y1]
pattan_lines.append(line)
return pattan_lines
def _trim_lines(self,pattan_lines):
trim_lines = []
nodes = self.path.nodes + [self.path.nodes[0]]
for line in pattan_lines:
x0,y0,x1,y1 = line
cross_points = self.crossPointsOfPath(line)
p0_in_path = self.isPointInPath(x0,y0)
p1_in_path = self.isPointInPath(x1,y1)
cnt = len(cross_points)
if cnt == 0:
if p0_in_path and p1_in_path:
trim_lines.append(line)
pass
elif cnt == 1:
p = cross_points[0]
if p0_in_path:
line = (x0,y0,p[0],p[1])
else:
line = (p[0],p[1],x1,y1)
pass
trim_lines.append(line)
else:
p = [(x0,y0)]+cross_points+[(x1,y1)]
p.sort()
if p0_in_path:
in_path = True
else:
in_path = False
for i in range(len(cross_points)+1):
if in_path:
line = (p[i][0],p[i][1],p[i+1][0],p[i+1][1])
trim_lines.append(line)
if in_path:
in_path = False
else:
in_path = True
self.cross_points += cross_points
return trim_lines
def _tile_fill(self,x,y,array):
array[x][y] = 1
if y-1 > 0:
if array[x][y-1]==0:
array = self._tile_fill(x,y-1,array)
if x+1 < self.xn:
if array[x+1][y]==0:
array = self._tile_fill(x+1,y,array)
if y+1 < self.yn:
if array[x][y+1]==0:
array = self._tile_fill(x,y+1,array)
if x-1 > 0:
if array[x-1][y]==0:
array = self._tile_fill(x-1,y,array)
if x==0 or y==0 or x==self.xn-1 or y==self.yn-1:
self._bflag = True
return array
def isPointInPath(self,x,y):
nodes = self.path.nodes + [self.path.nodes[0]]
cross_points = []
line = (0,1,-y)
pts = self.crossPointsOfPath(line)
for p in pts:
if x < p[0]:
cross_points.append(p)
if len(cross_points) % 2 == 1:
return True
else:
return False
def crossPointsOfPath(self,line):
# line = [x0,y0,x1,y1] or [p0,p1] or [a,b,c]
cnt = len(line)
if cnt == 2:
x0,y0 = line[0]
x1,y1 = line[1]
line_eq = line_generalization(line[0],line[1])
elif cnt == 3:
line_eq = line
elif cnt == 4:
x0,y0,x1,y1 = line
line_eq = line_generalization((x0,y0),(x1,y1))
cross_points = []
nodes = self.path.nodes + [self.path.nodes[0]]
m = 0.000001
for k in range(len(self.path.nodes)):
p0 = nodes[k].p
p1 = nodes[k].p1
p2 = nodes[k+1].p0
p3 = nodes[k+1].p
if nodes[k].p1_avoid and nodes[k+1].p0_avoid:
ps = intersection_of_line_segment(p0,p3,line_eq)
else:
ps = intersection_of_bezier_and_line((p0,p1,p2,p3),line_eq)
if cnt == 3: #no limit line lengh
cross_points += ps
else:
for p in ps:
xmax,xmin = max((x0,x1)),min(x0,x1)
ymax,ymin = max((y0,y1)),min(y0,y1)
if (xmin-m <= p[0] and p[0] <= xmax+m and
ymin-m <= p[1] and p[1] <= ymax+m):
cross_points.append(p)
return cross_points
def intersection_of_line_segment((x0,y0),(x1,y1),(a,b,c)):
line = line_generalization((x0,y0),(x1,y1))
points = intersection_2line(line,(a,b,c))
m = 0.000001
xs = [x0,x1]
ys = [y0,y1]
new_points = []
for p in points:
if (min(xs)-m <= p[0] and p[0] <= max(xs)+m and
min(ys)-m <= p[1] and p[1] <= max(ys)+m):
new_points.append(p)
return new_points
def intersection_2line((a0,b0,c0),(a1,b1,c1)):
t = float(a0*b1-a1*b0)
if t == 0:
return []
x = (b0*c1-b1*c0)/t
y = (a1*c0-a0*c1)/t
return [(x,y)]
def intersection_of_bezier_and_line((p0,p1,p2,p3),(a,b,c)):
f0 = a * p0[0] + b * p0[1] + c
f1 = 3 * (a * p1[0] + b * p1[1] + c)
f2 = 3 * (a * p2[0] + b * p2[1] + c)
f3 = a * p3[0] + b * p3[1] + c
_a = -f0 + f1 - f2 + f3
_b = 3 * f0 - 2 * f1 + f2
_c = -3 * f0 + f1
_d = f0
if _a == 0:
if _b == 0:
if _c == 0: tlist = []
else: tlist = -_d/_c
else:
tlist = quadratic_equation(_b,_c,_d)
else:
tlist = cubic_equation(_a,_b,_c,_d)
points = []
for t in tlist:
if t < 0 or 1 < t:
continue
x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
points.append((x,y))
return points
def cubic_equation(a,b,c,d):
p = -b**2/(9.0*a**2) + c/(3.0*a)
q = b**3/(27.0*a**3) - b*c/(6.0*a**2) + d/(2.0*a)
t = complex(q**2+p**3)
w =(-1.0 +1j*3.0**0.5)/2.0
u = [0,0,0]
u[0] = (-q +t**0.5)**(1.0/3.0)
u[1] = u[0] * w
u[2] = u[0] * w**2
v = [0,0,0]
v[0] = (-q -t**0.5)**(1.0/3.0)
v[1] = v[0] * w
v[2] = v[0] * w**2
x_list = []
for i in range(3):
for j in range(3):
if abs(u[i]*v[j] + p) < 0.0001:
x = u[i] + v[j]
if abs(x.imag) < 0.0000001:
x = x.real - b/(3.0*a)
x_list.append(x)
return x_list
def quadratic_equation(a,b,c):
d = b*b-4*a*c
if d < 0:
return []
if d == 0:
x = -b/(2.0*a)
return [x]
else:
x0 = (-b+d**0.5)/(2.0*a)
x1 = (-b-d**0.5)/(2.0*a)
return [x0,x1]
def line_generalization(p0,p1):
if p0[0] == p1[0]:
a = 1.0
b = 0.0
c = float(-p0[0])
elif p0[1] == p1[1]:
a = 0.0
b = 1.0
c = float(-p0[1])
else:
slope = float(p1[1]-p0[1])/(p1[0]-p0[0])
intercept = p0[1] - slope*p0[0]
a = slope
b = -1.0
c = intercept
return a,b,c
def main():
window = Tkinter.Tk()
canvas = Tkinter.Canvas(window,width=300,height=200)
canvas.pack()
n0 = Node([20,50],[30,10],[10,100])
n1 = Node([50,180],[20,170],[80,190])
n2 = Node([140,100],[50,90],[120,190])
n3 = Node([280,70],[250,150],[220,10])
path = Path([n0,n1,n2,n3])
path.closed = True
n1.p1_avoid = True
n2.p0_avoid = True
path.pattan = PattanTile(path)
if path.closed:
canvas.create_polygon(path.points(),fill='gray',outline='red')
else:
canvas.create_line(path.points(),fill='red')
r = 3
for n in path.nodes:
canvas.create_oval(n.p[0]-r,n.p[1]-r,n.p[0]+r,n.p[1]+r)
canvas.create_oval(n.p0[0]-r,n.p0[1]-r,n.p0[0]+r,n.p0[1]+r)
canvas.create_oval(n.p1[0]-r,n.p1[1]-r,n.p1[0]+r,n.p1[1]+r)
canvas.create_line(n.p[0],n.p[1],n.p0[0],n.p0[1])
canvas.create_line(n.p[0],n.p[1],n.p1[0],n.p1[1])
for xy in path.pattan.lines:
canvas.create_line(xy,fill='blue')
r = 2
for p in path.pattan.cross_points:
#canvas.create_oval(p[0]-r,p[1]-r,p[0]+r,p[1]+r)
pass
window.mainloop()
if __name__ == '__main__':
main()