さて、前回こしらえた点と点をベジェ曲線で結ぶ自前のパスをブーリアン演算で差分を取りたいと言っていたのはどうなったのか。できました、一応。
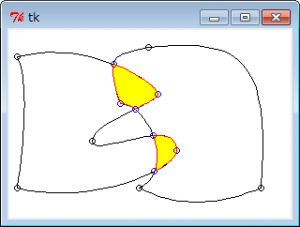
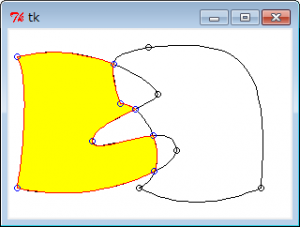
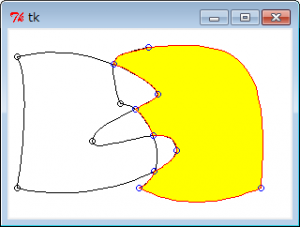
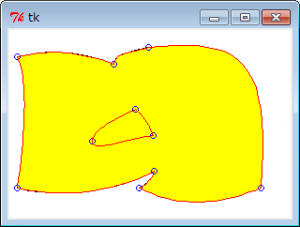
ソースは一番最後
まぁ、最後の合成は余分なパスを生成してるけど、ご愛嬌ってことで。
以下、よもやまプログラミング話。
点と点をベジェ曲線で結んでいるから交差判定は違うけど、きっと、ポリゴン(多角形)のブーリアン演算は共有するところが多いはずだよね。ってことで、まずは既存のアルゴリズムを探し漁りました。Wikiによると、代表的なアルゴリズムは以下の3つ。
・Vattiクリッピング法
・Sutherland–Hodgman法
・Weiler–Athertonクリッピング法
下2つは特殊ケースのアルゴリズムと書かれているので、おそらくベーシックなのは、一番上のVattiクリッピング法という方法なのでしょう。だがしかし、日本語の情報が見つからない。
Vatti Polygon Clipping
オープンソースのライブラリ
http://www.angusj.com/delphi/clipper.php
Vattiと違うのかもわかりませんが、他の日本語の解説してくれてるページを発見。んー、なんとなく曲線パスへの転用が難しそう。。。
平面図形の論理演算(ブーリアン)処理
http://www7b.biglobe.ne.jp/~garaku/Boolean.html
第9回 凸多角形の交差計算(前編)
http://gihyo.jp/dev/serial/01/geometry/0009
んー、自分で考えたものでも、案外上手くいくんじゃね?っといういつもの取り敢えずやってみよう精神で考えてみました。
パスとパスをつなぐセグメントに対する交点を順番に探していって、相手の内側にあるならそのセグメントをリストに追加っといった処理を繰り返して、閉領域を探し出します。
パス内にいる時リストに加えるのか、パス外にいる時に加えるのかで、合成するのか差分するのかを選択できます。
ただし、問題があって、困った事に閉じたパスを前提で考えしまったので、開いたパスは対応していません。(内側にいるとき、交点を通れば必ず外側になるっということを前提としているので)
その他、最後パスAとパスBそれぞれの処理の中で、全く同じ交点探索を繰り返してたり、明らかに無駄な部分もあったり、自己交差は考えてなかったり、色々と問題があるのですが、意欲も失せてにきたのでこの辺で・・・。
この中で、ベジェ曲線同士の交点とか、ベジェ曲線の分割とか要所のコードは備忘録サイトの方にまとめています。
http://code.tiblab.net/python/calculate/
ほぼ先人のコピペです。数学がてんで駄目の僕でも、人の知識を借りて、こうした処理ができるのだから、ウェブ社会素晴らしい。
そして、本当に素晴らしいのは、こうやって自前でコードを書かなくても、matplotlibやshapelyと言ったライブラリでできちゃうってことさ!
そう、もはや頑張ってアルゴリズムを考えて、実装する必要なんてなかった。後で知ったー。。。orz
# -*- coding: utf-8 -*-
import Tkinter
class Node:
p = [0.0,0.0] #self point
p0 = [0.0,0.0] #control point
p1 = [0.0,0.0] #control point
p0_avoid = False
p1_avoid = False
def __init__(self,p,p0,p1,p0_avoid=False,p1_avoid=False):
self.p = p
self.p0 = p0
self.p1 = p1
self.p0_avoid = p0_avoid
self.p1_avoid = p1_avoid
class Path:
nodes = []
closed = False
steps = 20
fill_color = ''
line_color = 'black'
node_color = 'black'
point_color = 'gray'
def __init__(self,nodes = None):
if nodes == None:
return
self.nodes = nodes
def points(self):
if len(self.nodes) == 0:
return []
points = []
points.append(self.nodes[0].p)
for i in range(1,len(self.nodes)):
points += self.segment_points(i-1,i)
if self.closed:
points += self.segment_points(i,0)
points = points[:-1]
return points
def segment_points(self,i,j):
points = []
n0 = self.nodes[i]
n1 = self.nodes[j]
if n0.p1_avoid == True and n1.p0_avoid == True:
points.append(n1.p)
else:
pts = bezier_points(n0.p,n0.p1,n1.p0,n1.p,self.steps)
points += pts[1:]
return points
def segment(self,i):
j = i + 1
if len(self.nodes) <= j:
j = j - len(self.nodes)
p0 = self.nodes[i].p
p1 = self.nodes[i].p1
p2 = self.nodes[j].p0
p3 = self.nodes[j].p
if self.nodes[i].p1_avoid and self.nodes[j].p0_avoid:
segment = [p0,p3]
else:
segment = [p0,p1,p2,p3]
return segment
def boundary(self):
cnt = len(self.nodes)
if not self.closed:
cnt -= 1
f = float('inf')
bound = [f,f,-f,-f]
for i in range(cnt):
segment = self.segment(i)
if len(segment) == 2:
p0,p1 = segment
xmin = min(p0[0],p1[0])
xmax = max(p0[0],p1[0])
ymin = min(p0[1],p1[1])
ymax = max(p0[1],p1[1])
else:
p0,p1,p2,p3 = segment
xmin,ymin,xmax,ymax = bezeir_boundary(p0,p1,p2,p3)
if xmin < bound[0]:
bound[0] = xmin
if ymin < bound[1]:
bound[1] = ymin
if bound[2] < xmax:
bound[2] = xmax
if bound[3] < ymax:
bound[3] = ymax
return bound #xmin,ymin,xmax,ymax
def is_clockwise(self):
total = 0.0
for i in range(len(self.nodes)-1):
p0 = self.nodes[i].p
p1 = self.nodes[i+1].p
total += p0[0] * p1[1] - p1[0] * p0[1]
if total > 0:
return True
else:
return False
def reverse(self):
new_nodes = []
for i in range(len(self.nodes)-1,-1,-1):
node = self.nodes[i]
p = node.p
p0 = node.p1
p1 = node.p0
n = Node(p,p0,p1)
new_nodes.append(n)
self.nodes = new_nodes
return
def is_inside(self,x,y):
if not self.closed:
return False
nodes = self.nodes + [self.nodes[0]]
box = self.boundary()
p0 = (x,y)
p1 = (box[2]+10,y)
line = (p0,p1)
cross_points = self.cross_points(line)
if len(cross_points) % 2 == 1:
return True
else:
return False
def cross_points(self,line):
# line = [p0,p1] or [a,b,c]
cnt = len(self.nodes)
cross_points = []
if not self.closed:
cnt -= 1
for i in range(cnt):
seg = self.segment(i)
ps = intersection_of_segments(seg,line,True)
cross_points += ps
return cross_points
debug_segments = []
debug_points = []
def boolean_paths(path0,path1,disc0,disc1):
global debug_segments,debug_points
path = [path0,path1]
for i in [0,1]:
if path[i].is_clockwise():
path[i].reverse()
group0 = boolean_segments(path0,path1,disc0)
group1 = boolean_segments(path1,path0,disc1)
group1.reverse()
if len(group0) != len(group1):
print('Error path_boolean() 1')
#return []
#group1 reverse
if disc0 != disc1:
for segments in group1:
for segment in segments:
segment.reverse()
segments.reverse()
#debug
for group in [group0,group1]:
for segments in group:
for segment in segments:
debug_segments.append(segment)
#group1 sort
find = False
p0 = group0[0][-1][-1]
for i in range(len(group1)):
p1 = group1[i][0][0]
if is_same_point(p0,p1):
find = True
break
if find:
group1 = group1[i:]+group1[:i]
else:
print('Error path_boolean() 2')
return []
#join group0 and group1
group = []
segments = []
start_point = None
for i in range(len(group0)):
segments0 = group0[i]
segments1 = group1[i]
segments += segments0 + segments1
if not start_point:
start_point = segments[0][0]
last_point = segments[-1][-1]
if is_same_point(start_point,last_point):
group.append(segments)
segments = []
if len(segments) > 0:
group.append(segments)
#make path
paths = []
for i in range(len(group)):
is_added = True
nodes = []
for j in range(len(group[i])):
segments = group[i]
s0 = segments[j-1]
s1 = segments[j]
if not is_same_point(s0[-1],s1[0]):
print('Error path_boolean() 3')
return []
p = s1[0]
for k in [0,1]:
if not path[k].closed:
if(is_same_point(p,path[k].nodes[0].p) or
is_same_point(p,path[k].nodes[-1].p)):
is_added = False
break
if len(s0) == 2:
_p0,_p1 = s0
x = _p0[0] + 0.75*(_p1[0] - _p0[0])
y = _p0[1] + 0.75*(_p1[1] - _p0[1])
p0 = (x,y)
p0_avoid = True
else:
p0 = s0[2]
p0_avoid = False
if len(s1) == 2:
_p0,_p1 = s1
x = _p0[0] + 0.25*(_p1[0] - _p0[0])
y = _p0[1] + 0.25*(_p1[1] - _p0[1])
p1 = (x,y)
p1_avoid = True
else:
p1 = s1[1]
p1_avoid = False
nodes.append(Node(p,p0,p1,p0_avoid,p1_avoid))
if is_added:
new_path = Path(nodes)
new_path.closed = True
paths.append(new_path)
return paths
def boolean_segments(path0,path1,disc):
groups = []
segments = []
cnt0 = len(path0.nodes)
cnt1 = len(path1.nodes)
## if not path0.closed:
## cnt0 -= 1
## if not path1.closed:
## cnt1 -= 1
is_inside = path1.is_inside(*path0.nodes[0].p)
for i in range(cnt0):
seg0 = path0.segment(i)
tlist = []
for j in range(cnt1):
seg1 = path1.segment(j)
ts = intersection_of_segments(seg0,seg1,False)
for t in ts:
tlist.append(t[0])
if len(tlist) > 0:
tlist.sort()
pre_t = 0.0
for t in tlist:
_t = (t-pre_t)/(1.0-pre_t)
s0,s1 = segment_split(seg0,_t)
if is_inside == disc:
segments.append(s0)
groups.append(segments)
segments = []
if is_inside:
is_inside = False
else:
is_inside = True
pre_t = t
seg0 = s1
if is_inside == disc:
segments.append(s1)
else: #if not crossed
if is_inside == disc:
segments.append(seg0)
if len(segments)>0:
groups[0] = segments + groups[0]
return groups
def is_same_point(p0,p1):
x0,y0 = p0
x1,y1 = p1
s = abs(x1-x0)+abs(y1-y0)
if s < 0.00001:
return True
else:
return False
def segment_split(segment,t):
#segment = (p0,p1)[line] or (p0,p1,p2,p3)[bezier]
n = len(segment)
if n == 2: #if line
return line_split(segment,t)
elif n == 4:
return bezier_split(segment,t)
def point_on_line((p0,p1),t):
x = p0[0] + t*(p1[0] - p0[0])
y = p0[1] + t*(p1[1] - p0[1])
return (x,y)
def line_generalization(p0,p1):
if p0[0] == p1[0]:
a = 1.0
b = 0.0
c = float(-p0[0])
elif p0[1] == p1[1]:
a = 0.0
b = 1.0
c = float(-p0[1])
else:
slope = float(p1[1]-p0[1])/(p1[0]-p0[0])
intercept = p0[1] - slope*p0[0]
a = slope
b = -1.0
c = intercept
return a,b,c
def line_split((p0,p1),t):
p = point_on_line((p0,p1),t)
return [[p0,p],[p,p1]]
def bezier_point((p0,p1,p2,p3),t):
x = (1-t)**3*p0[0]+3*(1-t)**2*t*p1[0]+3*(1-t)*t**2*p2[0]+t**3*p3[0]
y = (1-t)**3*p0[1]+3*(1-t)**2*t*p1[1]+3*(1-t)*t**2*p2[1]+t**3*p3[1]
return (x,y)
def bezier_points(p0,p1,p2,p3,steps=20):
points = []
for i in range(steps+1):
t = i/float(steps)
p = bezier_point((p0,p1,p2,p3),t)
points.append(p)
return points
def bezeir_boundary(p0,p1,p2,p3):
bounds = [[],[]]
bounds[0] += [p0[0],p3[0]]
bounds[1] += [p0[1],p3[1]]
for i in [0,1]:
a = float(-3*p0[i] + 9*p1[i] - 9*p2[i] + 3*p3[i])
b = float( 6*p0[i] - 12*p1[i] + 6*p2[i])
c = float( 3*p1[i] - 3*p0[i])
if a == 0:
if b == 0: continue
tlist = [-c / b]
else:
tlist = quadratic_equation(a,b,c)
for t in tlist:
if 0 < t < 1:
v = (1-t)**3*p0[i] + 3*(1-t)**2*t*p1[i] + 3*(1-t)*t**2*p2[i] + t**3*p3[i]
bounds[i].append(v)
return [min(bounds[0]),min(bounds[1]),
max(bounds[0]),max(bounds[1])]
def bezier_split(points,t):
if not 0 < t < 1:
print('Error bezier_split(): t must be 0 xmax1 or xmax0 < xmin1 or
ymin0 > ymax1 or ymax0 < ymin1): #if overlap
b0,b1 = bezier_split(bezier0,0.5)
b2,b3 = bezier_split(bezier1,0.5)
c0 = [b0,t0,(t1+t0)/2]
c1 = [b1,(t1+t0)/2,t1]
c2 = [b2,t2,(t3+t2)/2]
c3 = [b3,(t3+t2)/2,t3]
buff += [[c0,c2],[c0,c3],[c1,c2],[c1,c3]]
if len(buff) == 0:
break
if n == 9999:
print('Error intersection_of_bezier_curves(): cannot convergence.')
return []
#marge
groups = []
for t in result:
is_included = False
for group in groups:
d0 = abs(group[0][0]-t[0])
d1 = abs(group[0][1]-t[1])
if d0 < 0.00001 and d1 < 0.00001:
is_included = True
continue
if is_included:
group.append(t)
else:
groups.append([t])
result = []
for group in groups:
t = [0,0]
for _t in group:
for i in range(2):
t[i] += _t[i]
for i in range(2):
t[i] = t[i]/len(group)
result.append(t)
#print(str(len(position))+' points found.')
return result
def intersection_of_bezier_and_line((p0,p1,p2,p3),line,return_coord=True):
#line = (a,b,c) or (p0,p1)
if len(line) == 2:
a,b,c = line_generalization(*line)
else:
a,b,c = line
f0 = a * p0[0] + b * p0[1] + c
f1 = 3 * (a * p1[0] + b * p1[1] + c)
f2 = 3 * (a * p2[0] + b * p2[1] + c)
f3 = a * p3[0] + b * p3[1] + c
_a = -f0 + f1 - f2 + f3
_b = 3 * f0 - 2 * f1 + f2
_c = -3 * f0 + f1
_d = f0
if _a == 0:
if _b == 0:
if _c == 0: tlist = []
else: tlist = [-_d/_c]
else:
tlist = quadratic_equation(_b,_c,_d)
else:
tlist = cubic_equation(_a,_b,_c,_d)
result = []
for t in tlist:
if t < 0 or 1 < t:
continue
x,y = bezier_point((p0,p1,p2,p3),t)
if len(line) == 2:
p0,p1 = line
xmin = min(line[0][0],line[1][0])
xmax = max(line[0][0],line[1][0])
if x < xmin or xmax < x:
continue
if return_coord:
result.append([x,y])
else:
if len(line) == 2:
t1 = (x-p0[0])/(p1[0]-p0[0])
else:
t1 = 1.0
result.append([t,t1])
return result
def intersection_of_lines(line0,line1,return_coord=True):
#line = (p0,p1) or (a,b,c)
lines = [line0,line1]
line_n = [len(line0),len(line1)]
for i in range(2):
if line_n[i] == 3:
a,b,c = lines[i]
if a == 0:
x0 = x1 = 0
y0 = y1 = -c/b
elif b == 0:
x0 = x1 = -c/a
y0 = y1 = 0
else:
x0 = 0.0
x1 = 1.0
y0 = -c/b
y1 = (-a-c)/b
lines[i] = [(x0,y0),(x1,y1)]
p0,p1 = lines[0]
p2,p3 = lines[1]
d = float((p1[0]-p0[0])*(p3[1]-p2[1])-(p1[1]-p0[1])*(p3[0]-p2[0]))
if d == 0:
return []
ac = (p2[0]-p0[0],p2[1]-p0[1])
t0 = ((p3[1]-p2[1])*ac[0] - (p3[0]-p2[0])*ac[1]) / d
t1 = ((p1[1]-p0[1])*ac[0] - (p1[0]-p0[0])*ac[1]) / d
if line_n[0] == 2:
if t0 < 0 or 1 < t0:
return []
if line_n[1] == 2:
if t1 < 0 or 1 < t1:
return []
x = p0[0] + t0*(p1[0] - p0[0])
y = p0[1] + t0*(p1[1] - p0[1])
if return_coord:
return [[x,y]]
else:
return [[t0,t1]]
def cubic_equation(a,b,c,d):
p = -b**2/(9.0*a**2) + c/(3.0*a)
q = b**3/(27.0*a**3) - b*c/(6.0*a**2) + d/(2.0*a)
t = complex(q**2+p**3)
w =(-1.0 +1j*3.0**0.5)/2.0
u = [0,0,0]
u[0] = (-q +t**0.5)**(1.0/3.0)
u[1] = u[0] * w
u[2] = u[0] * w**2
v = [0,0,0]
v[0] = (-q -t**0.5)**(1.0/3.0)
v[1] = v[0] * w
v[2] = v[0] * w**2
x_list = []
for i in range(3):
for j in range(3):
if abs(u[i]*v[j] + p) < 0.0001:
x = u[i] + v[j]
if abs(x.imag) < 0.0000001:
x = x.real - b/(3.0*a)
x_list.append(x)
return x_list
def quadratic_equation(a,b,c):
d = b*b-4*a*c
if d < 0:
return []
if d == 0:
x = -b/(2.0*a)
return [x]
else:
x0 = (-b+d**0.5)/(2.0*a)
x1 = (-b-d**0.5)/(2.0*a)
return [x0,x1]
def main():
window = Tkinter.Tk()
canvas = Tkinter.Canvas(window,width=300,height=200,bg='white')
canvas.pack()
n0 = Node([10,30],[90,10],[20,50])
n1 = Node([10,170],[20,100],[90,190])
n2 = Node([180,130],[180,160],[180,90])
n7 = Node([90,120],[90,140],[90,100])
n8 = Node([160,70],[160,80],[160,60])
n3 = Node([150,20],[250,10],[120,30])
n4 = Node([120,80],[100,20],[150,80])
n5 = Node([140,170],[180,150],[180,190])
n6 = Node([270,170],[220,190],[280,30])
path0 = Path([n0,n1,n2,n7,n8])
path0.closed = True
n1.p1_avoid = True
n2.p0_avoid = True
path1 = Path([n3,n4,n5,n6])
path1.closed = True
#n3.p1_avoid = True
#n4.p0_avoid = True
bpaths = boolean_paths(path0,path1,True,True)
for path in bpaths:
path.fill_color = 'yellow'
path.point_color = ''
path.node_color = 'red'
path.line_color = 'red'
paths = [path0,path1]+bpaths
r = 3
for path in paths:
if path.closed:
canvas.create_polygon(path.points(),fill=path.fill_color,outline=path.line_color)
for n in path.nodes:
canvas.create_oval(n.p[0]-r,n.p[1]-r,n.p[0]+r,n.p[1]+r,outline=path.node_color)
canvas.create_oval(n.p0[0]-r,n.p0[1]-r,n.p0[0]+r,n.p0[1]+r,outline=path.point_color)
canvas.create_oval(n.p1[0]-r,n.p1[1]-r,n.p1[0]+r,n.p1[1]+r,outline=path.point_color)
canvas.create_line(n.p[0],n.p[1],n.p0[0],n.p0[1],fill=path.point_color)
canvas.create_line(n.p[0],n.p[1],n.p1[0],n.p1[1],fill=path.point_color)
canvas.create_line(path.points(),fill=path.line_color)
for p in debug_points:
#canvas.create_oval(p[0]-r,p[1]-r,p[0]+r,p[1]+r,outline='red')
pass
for seg in debug_segments:
if len(seg) == 4:
ps = bezier_points(*seg)
else:
ps = seg
#canvas.create_line(ps,fill='red',arrow=Tkinter.LAST)
window.mainloop()
if __name__ == '__main__':
main()
