前回、温湿度センサーDHT20で温度を取得しましたが、今回はサーミスタで温度を取得します。

使用したサーミスタは下記で1本15円。何かと測りたい温度測定のコストを下げたいなと思って。
サーミスタ 10kΩ (10本入)¥150
https://akizukidenshi.com/catalog/g/gP-17250/
実のところ、DHT20はこの温度校正がしたくて買いました。
■ 回路
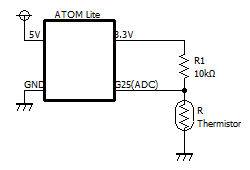
本サーミスタを10kΩの抵抗で分圧しました。
【パーツ】
・M5stack ATOM Lite
・サーミスタDKF103*1
・抵抗R1 10kΩ
■ プログラム
【ソースコード(MicroPython)】
import machine
import utime
import math
adc = machine.ADC(machine.Pin(33))
adc.atten(machine.ADC.ATTN_11DB)
# サーミスタの設定
B = 3960 #B定数
To = 25 #基準温度
Ro = 10000 #基準温度時の抵抗値
# 回路の設定
Vcc = 3.3 #入力電圧
R1 = 10000 #分圧抵抗
Vout = adc.read_u16()* 3.3/65535
R = R1 * Vout/(Vcc-Vout)
T = 1/(1/(To+273.15)+math.log(R/Ro)/B)-273.15
print("Temp: " + str(T))
参考サイト:アナログ温度センサ4 サーミスタ
https://www.denshi.club/pc/raspi/5raspberry-pi-zeroiot-4.html
【解説】
サーミスタ、正確にはNTCサーミスタと呼ばれる素子で、温度で抵抗が変化して、その式が以下です。
R = Ro * math.exp(B*( 1/(T+273.15) - 1/(To+273.15) ))
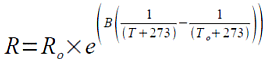
温度Tの形にした式が以下。
T =1/(1/(To+273.15)+math.log(R/Ro)/B)-273.15
Toは基準温度、Roは基準温度時の抵抗値、BはB定数でデータシートから得られます。
今回のDKF103*1の場合、T0=25℃、Ro=10000Ω、B=3960です。
あとは分圧式から抵抗値を算出します。
R = R1 * Vout/(Vcc-Vout)
R1は分圧した抵抗、Vccは入力電圧、VoutはATOM LiteのADコンバータで取得した電圧です。分圧する抵抗は、温度の測定範囲とADコンバータの測定範囲に応じて決めます。
上式は対数の計算が必要で、MicroPythonはmathモジュールで手軽に計算できるので問題ないですが、PICなどのマイコンだと対数の計算をするのは手間なので、線形近似するのが、よくあるやり方だそうです。
温度の測定範囲を-10℃〜50℃として、線形近似させてみました。
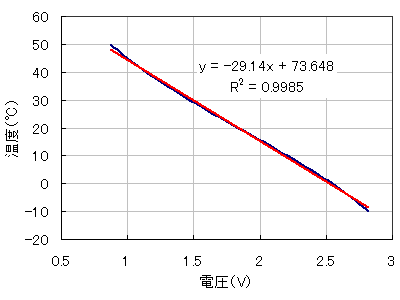
今回の条件では、近似式はy=-29.14x+73.648でした。xに取得電圧を代入すれば、温度を得られます。相関係数0.9985。こちらでも全然問題ないですね。
エクセルファイルを上げておくので良かったらどうぞ。
thermistor_linear_approx.xls
測定
室温で実際測ってみて、DHT20の測定結果と比較すると、けっこう差がありました。テスターで確認してみると、テスターで測る電圧とATOM Liteが認識している電圧に差があり、原因として、ノートPCのUSB供給の電圧が4.5Vと低めで、3.3V出力が2.9Vになってました。
また10kΩのカーボン抵抗が実測値だと9.82kΩだったので、それぞれのパラメータを実測値に合わせると、DHT20との差がほぼなくなりました。
ただモバイルバッテリーを電源にすると5V出力は5.1Vで、3.3V出力は3.2Vになり、電圧が変わります。電源の安定度合い、大事ですね。
ベランダで鉛蓄電池とDCDCコンバータを電源に、外気温を5分に1回、1日計測してみました。
DHT20と今回の回路に加え、何年か前に買ったIC温度計センサーLM61CIZを合わせて測定しました(測定したときの記事)。
ちなみに今の価格でDHT20が380円、LM61CIZが120円です。
その結果がこちら。
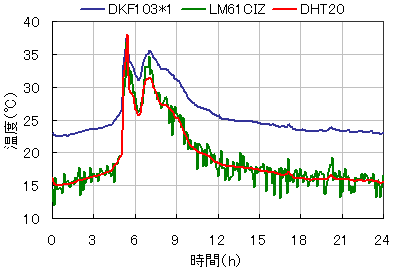
DHT20はさすが安定してます。LM61CIZは値がバラついていますが、値としてはDHT20と同じくらい。測定時1回しか計測しませんでしたが、100回の平均をとるなどすれば問題なさそうです。ATOM Lite(ESP32)のADCの誤差である程度ズレると思ってましたが、思いの外良かったです。
さて、肝心のサーミスタの方は、値はバラついてませんが、だいぶズレちゃってますね。
DHT20の温度との関係は下図となります。
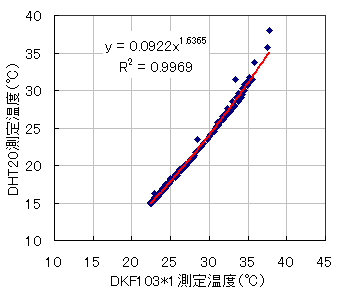
ちなみに直線近似すると、y=1.2763x-13.905(R^2=0.9924)でした。
直線や指数式で近似できるので、補正はできそうです。
補正するには、測定範囲を均等にデータを取った方が良いですが、差しあたっては使えますかね。いつか校正用のデータを取得したい。
